Preliminary: MoS

The previous work on breaking the softmax bottleneck is Mixture of Softmaxes (MoS). It breaks the SM bottleneck by not allowing the softmax to reduce the output to a low rank matrix. Instead they take a mixture of K softmaxes together. The MoS function is as follows:

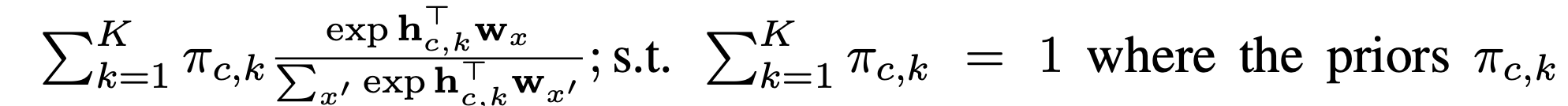
This formulation is not limited by the sm bottleneck because the log probability matrix is still high rank due to the log-sum-exp nonlinearity.

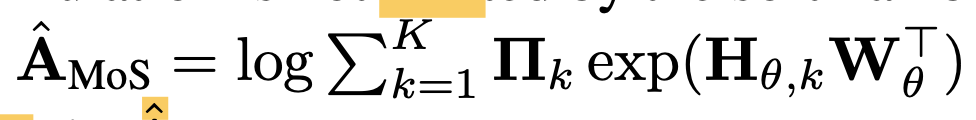
Logit space vector gating

The first key component to the papers contributions of breaking the sm bottleneck is Logit space vector gating. The most expensive part of MoS above is the K softmaxes that must be computed.

The papers key idea is to use vector gating instead of a scalar mixture, so mixture weights are not shared across different tokens. Formally it is below:

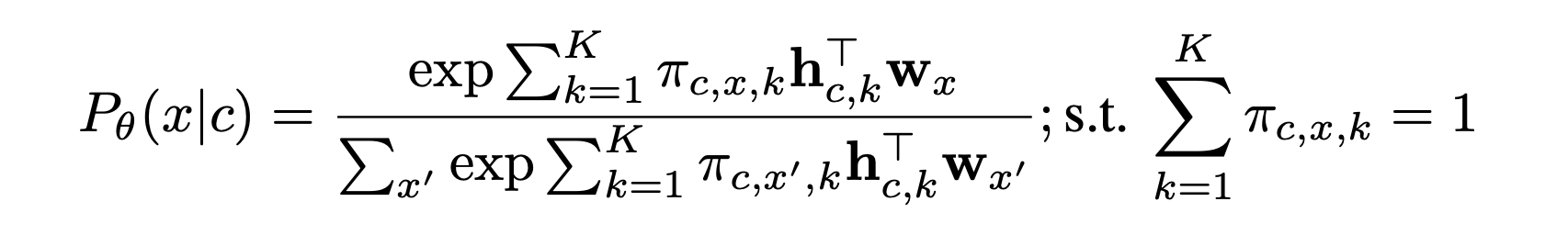
Due to the element-wise multiplication introduced the matrix factorization form that caused the sm bottleneck in the first place no longer applies.

There are still other efficiency techniques needed to be employed in order to gain efficiency over MoS, which we will look at tomorrow.